FFT调试有感

在电赛集训期间，调试FFT的代码时有感而发。

在电赛集训期间，我们主攻信号类题目，FFT是其中一个重要的工具。在调试FFT的代码时，渐渐有了一些以前没有的感受，或者说对以前模糊的感受有了更深的理解。
– > 理论中说烂了的频率在此基本不提，本文主要从更符合常人理解的角度来分析一下FFT的一些问题。

---

1. FFT的下标和最小分辨率

其实，FFT的下标就是这次FFT的最小分辨率，而对应的幅值就是在该最小分辨率的倍数处频率对应的幅值。
而最小分辨率的计算公式为：delta_f = maxIndex / N * fs

但虽然算是这么算，但是实际上由于不同设备的差异，实际的最小分辨率可能会有偏差。这对低频的影响其实不大，因为低频分量的周期实在够长，误差不会太大。但是对于高频分量来说，周期短，误差就会比较明显。

这其实也是理论推导和实际落地的差异。理论上，FFT的下标是一个理想的分辨率，但是实际中，由于设备的限制，可能会有偏差。

对此，其实我的处理方法也很简单。举个例子，比如我们现在最低分辨率预计10Hz，那此时对应的下标就是1。那么在10kHz时，下标理论上应该是1000，但是实际中可能会有偏差，比如990~1010。这时，就微调采样的周期，使得对应10kHz的下标刚好在1000处。

2. FFT频谱泄露原因

2.1 频谱泄露的小小分析

FFT频谱泄露其实是一个很老生常谈的话题了。其实网上很多的解释都只提及“截断的长度不为整数倍的周期所以导致了频谱泄露”。这没问题，但我觉得这解释并不完全和直观。而且这不能很好的解释为什么低频的频谱泄露不明显，而高频的频谱泄露很明显。

首先，我们要回顾FFT的来源。FFT其实是对离散傅里叶变换（DFT）的优化。而DFT其实是从DFS中截取的一个周期（DFS的时域和频域都是周期离散的）。所以，FFT计算后的结果对应的其实与DFS计算后的结果是直接相关的，其中的时域波形是周期波形的一个周期。

• 所以，由FFT计算得到的频谱分量，其实是对由于FFT采样的时域波形的周期延拓对应的无限长波形的频谱分量。

那这个时候我们再来回看一下前面提及的解释：截断的长度不为整数倍的周期所以导致了频谱泄露。我们对比输出的图片来分析以下
1. 输入信号频率较低，采样频率准确：

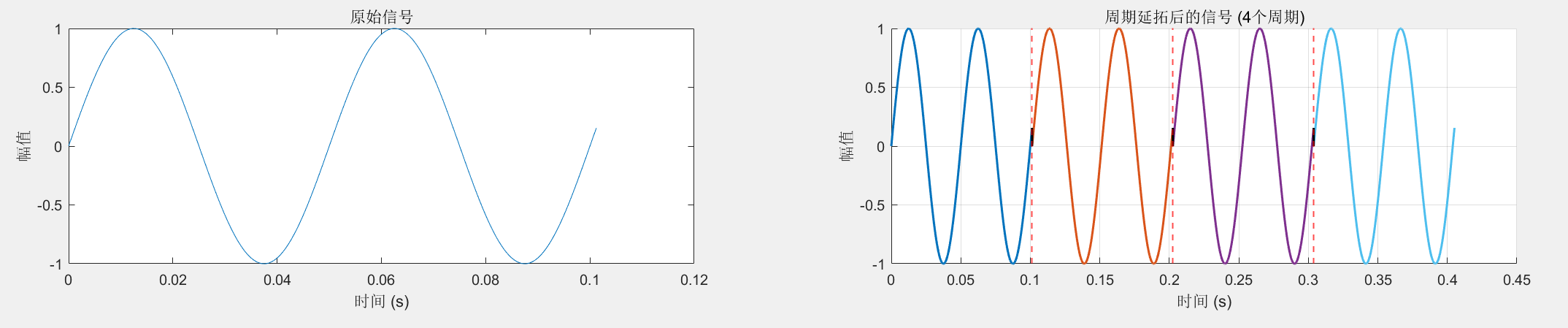
1. 输入信号频率较低，采样频率有偏差：

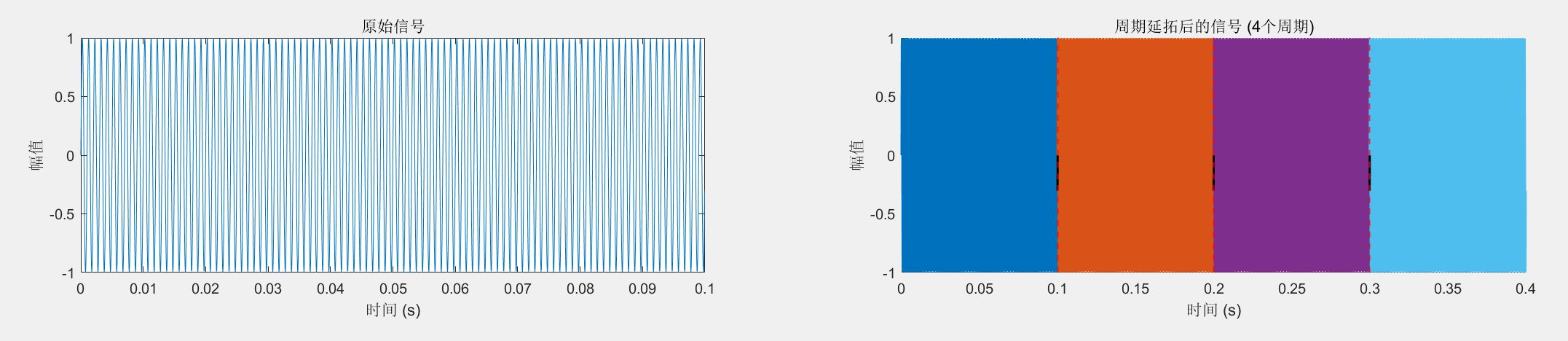
1. 输入信号频率较高，采样频率准确：


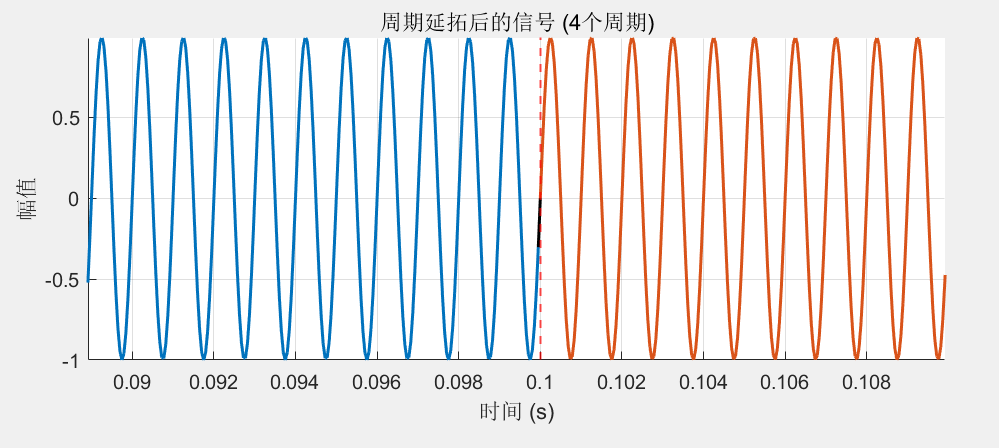
1. 输入信号频率较高，采样频率有偏差：

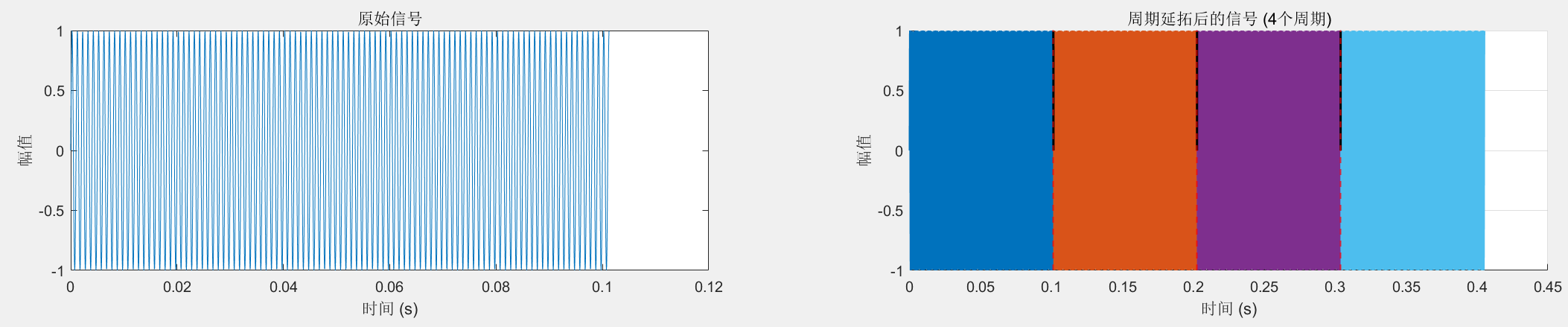
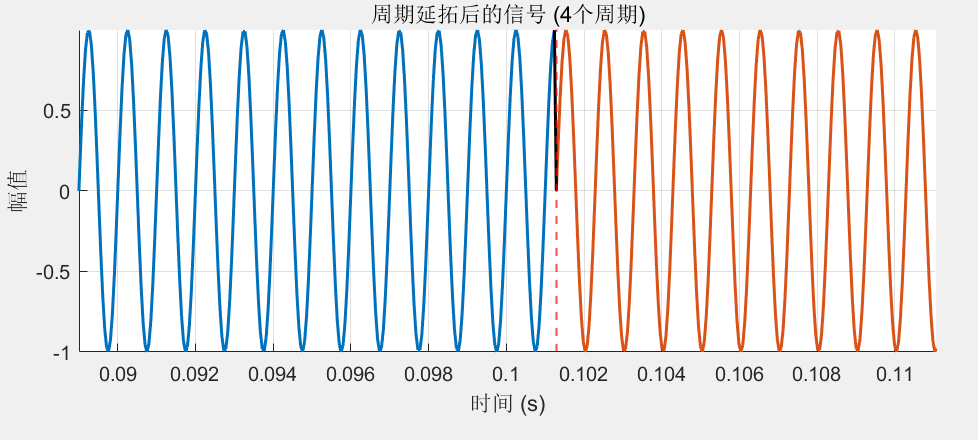
观察图片，可以发现，在低频的时候采样频率有偏差使得不为整数倍时，延拓后的周期在交界处相较于整个信号来说其实并不明显。而在高频的时候采样频率有偏差使得不为整数倍时，延拓后的周期在交界处相较于整个信号来说就非常明显了。

综上，我个人认为，这就是直观的高频频谱泄露比低频频谱泄露明显的解释。
而频谱泄露的直接原因，不是简简单单的“截断的长度不为整数倍的周期”导致的，而是其延拓后（即实际对应的DFS信号）不为连续变化，在交界处有“突变”导致的。

2.2 频谱泄露的处理方法

频谱泄露的处理方法有很多，网上也有很多介绍。这里我就不赘述了。
但当想通上述的原因后，很多频谱泄露的处理方法就变得更容易理解了。
1. 窗函数
为什么加窗可以减少频谱泄露？网络上很多的分析我个人是觉得不够“直观”的。
我们先来回顾一下窗函数的大致形状：在采样的起始和末尾处分量是一个较小的系数，中间较大，如图所示(一个汉明窗示例)。

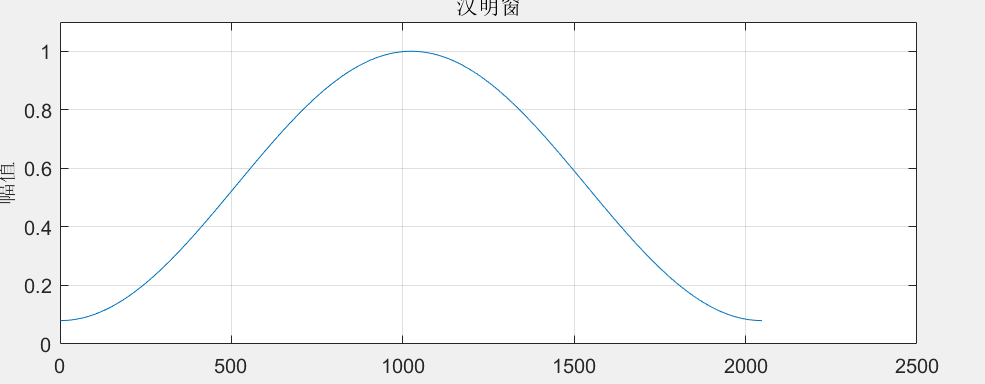
因为窗函数的作用就是对时域信号进行平滑处理，使得在交界处的突变变得不那么明显，从而减少频谱泄露。
– 窗函数的信号的影响：

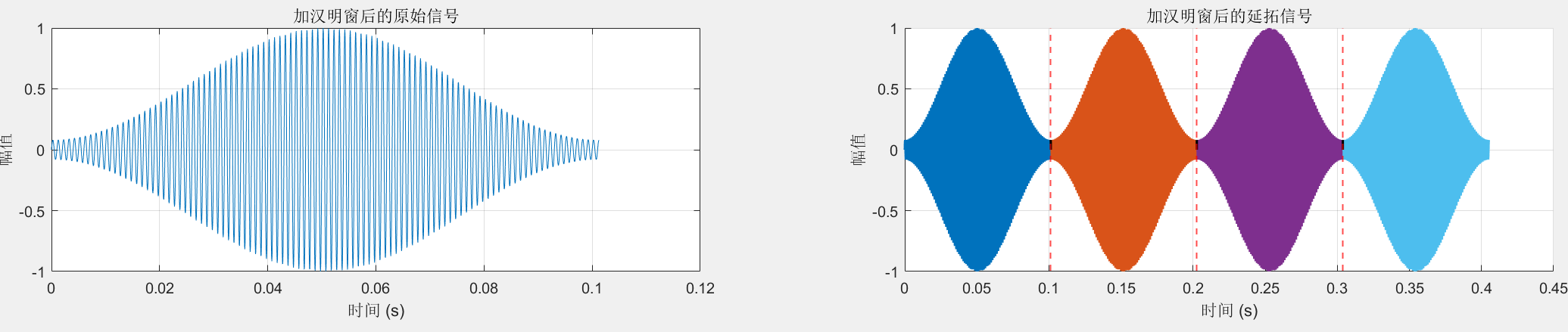
– 加窗后延拓信号交界处比较：

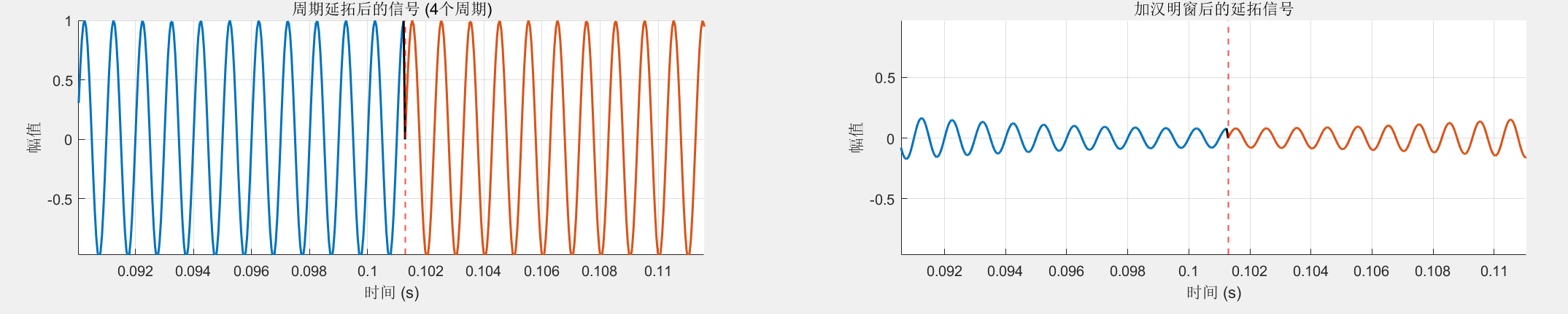
1. 采样频率的微调
   前文提及的采样频率微调，也可以减少频谱泄露。因为微调采样频率可以使得采样的时域波形对应的DFS信号的周期更接近整数倍，从而减少交界处的突变。

2. 频率矫正
   网上有些差值矫正算法，可以自己搜搜看，可以提高频率的分辨率或等等其它效果，自行了解吧。

3. 增加采样点数
   这是最暴力但其实也是最有效的方法。但是考虑到有些对实时性要求较高的场景，或者内存受限的场景，这个方法可能并不适用。

4. ap-fft
   全相位fft原理感兴趣可以参考这篇论文
   根据原理及这篇博客可以来编写ap-fft的相关算法
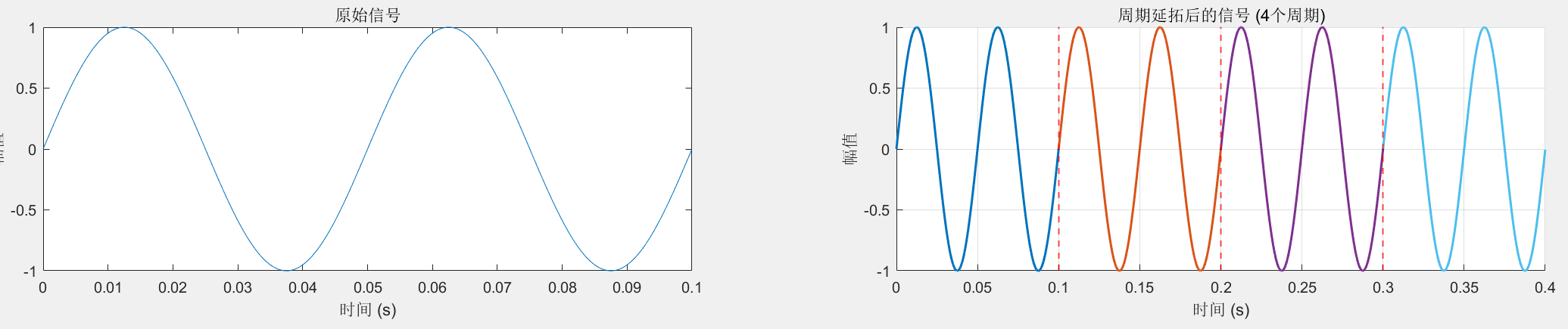
   我再matlab上进行了仿真对比，分别是2048点FFT、1024点FFT和2047个采样点的ap-fft，结果如下：
   

   
   
   上图中很坐标为索引，纵坐标为按照幅值进行的归一化处理后的幅值。可以看到，ap-fft的频谱泄露明显减少，甚至比2048点FFT还要好。不过ap-fft幅度上还是有些问题（因为这里的两个分量我是直接使用两个不同频率，但是幅值相同的分量，所以理应幅值一致。但是图中可以发现幅度有偏差）