简易神经网络推预测二阶Hs参数
2025.10.13 Keruone
Contents
前言
在今年电赛的G题中,任务是学习一个二阶未知网络的参数,并在自己的系统中复现其行为。
当时的做法是:采集该网络幅频和相频响应曲线中的若干数据点,通过SVD分解求伪逆,再利用最小二乘法重构出二阶传递函数 H(s) 的五个参数。
这一方法在PC端非常有效——无论是MATLAB还是Python,都能高效完成所需的矩阵运算。然而,一旦迁移到以C语言为主的嵌入式平台,问题就出现了:虽然理论上可以借助CMSIS等库实现基础矩阵操作,但SVD这类高阶线性代数运算往往不被支持;即便是像K230这样支持MicroPython的嵌入式设备,其Python环境也仅限于简单的矩阵运算,无法直接调用SVD等复杂功能。因此,原方案在资源受限的平台上难以落地。
受《深度学习入门:基于Python的理论与实现》和《深度学习进阶:自然语言处理》的启发,我意识到:一个轻量级神经网络理论上完全可以替代上述参数拟合过程。
更重要的是,这一思路的价值远不止于解决一道电赛题目。在未来的许多项目中,我们可能一时找不到合适的解析解,或者虽有理论方案却受限于目标平台的计算能力。而神经网络提供了一种灵活的替代路径——训练过程完全可以在PC上离线完成,嵌入式端只需部署训练好的参数,并执行前向推理所需的简单矩阵运算即可。这既规避了平台限制,又保留了模型的表达能力。
—
初版示例
整体逻辑框图
输入输出规划
以今年电赛G题的“学习部分”为例,输入输出的合理设计是整个方案成败的关键。合适的规划不仅能显著降低模型复杂度,还能提升泛化能力和部署效率。
最初,曾考虑让神经网络直接替代整个未知系统——即输入激励信号,输出响应信号。但这一思路存在明显缺陷:它要求训练过程也必须在嵌入式平台上完成,不仅受限于算力,还难以保证实时性与训练稳定性。
因此,转而采用参数回归的核心思路:让网络学习如何从幅频和相频响应中反推二阶传递函数 H(s) 的5个参数。这样一来,训练只需在PC端离线完成一次,嵌入式系统在运行时仅需调用已训练好的轻量模型进行推理,既保证了实时性,又规避了嵌入式端无法执行复杂训练的问题,从根本上解决了平台适配难题。
最终确定的输入输出结构如下:
- 输入:在1 kHz–10 kHz频段内,按对数均匀间隔选取32个频率点(该间隔方式可更均匀覆盖高低频特征,避免高频信息丢失),测量未知网络在这些点上的幅值和相位;随后将每个复数响应转换为实部与虚部,实部存入数组的
2*i位置,虚部存入2*i+1位置(通过固定索引规则确保数据映射的唯一性,降低模型学习难度),最终构成一个1×64的输入向量(批量训练时为N×64,批量模式可提升PC端训练效率)。 -
输出:一个
1×5的向量(批量时为N×5),对应二阶传递函数的五个待辨识参数,记为[a, b, c, d, e]。例如,可设
H(s) = \frac{a s^2 + b s + c}{s^2 + d s + e}
其中分母首项系数归一化为1(通过归一化减少参数冗余,降低模型收敛难度,同时确保参数辨识的唯一性),仅需辨识这五个参数即可完整描述系统的频域特性。
这种“频域特征 → 参数”的映射方式,既保留了明确的物理意义(每个输出参数对应传递函数的具体系数,便于后续系统复现与验证),又天然适配轻量神经网络的建模能力(输入维度可控、输出目标明确,无需复杂特征提取过程),为后续在资源受限设备上的部署奠定了核心基础。
损失函数规划
根据任务性质为连续值回归问题,选择 MSE 作为损失函数,具体如下:
class MSELoss:
"""
均方误差损失层(用于回归)
L = (1/N) * sum((y_pred - y_true)^2)
"""
def __init__(self):
self.params = []
self.grads = []
self.y_pred = None # 预测值
self.y_true = None # 真实值
def forward(self, y_pred, y_true):
"""
正向传播:计算 MSE 损失
args:
y_pred: 网络输出,形状 (N, 5)
y_true: 真实参数,形状 (N, 5)
return:
loss: 标量(平均损失)
"""
self.y_pred = y_pred
self.y_true = y_true
# 计算每个样本的平方误差,然后求平均
diff = y_pred - y_true
loss = np.mean(diff ** 2) # 等价于 np.sum(diff**2) / (N * 5)
return loss
之所以选用均方误差(MSE)作为损失函数,核心原因在于本任务属于典型的多输出回归问题:
网络需要预测的是五个连续实数参数([a, b, c, d, e]),而非类别标签。这些参数直接对应物理系统的传递函数系数,其取值范围无固定边界,且对精度敏感。
相比之下:
– Softmax + CrossEntropyLoss 适用于多分类任务,要求输出为概率分布且类别互斥;
– Sigmoid + Binary CrossEntropy 适用于二分类或多标签分类,输出被压缩到 [0,1] 区间;
– 而 CrossEntropy 系列损失函数本质上建模的是离散分布的差异,并不适合连续值的精确拟合。
在回归场景中,MSE 能直接度量预测值与真实值之间的欧氏距离平方,对误差敏感、梯度平滑,且与最小二乘法在统计意义上一致,天然契合参数辨识这类“从数据拟合连续参数”的目标。
此外,MSE 的计算简单、梯度明确(∂L/∂y_pred = 2*(y_pred - y_true)/N),便于在轻量级网络中实现反向传播,也利于后续在嵌入式端部署时进行简化或定点化处理。
因此,MSE 是本任务中最直接、合理且高效的选择。
参数预处理
训练参数生成与解参数预处理
在神经网络训练中,输入特征与输出标签的尺度和分布对收敛速度与精度有决定性影响。本任务中,五个待辨识参数([a, b, c, d, e])的物理量纲和数值范围差异极大:
– a 通常在 ±0.1 量级,
– b 约为 10^4,
– 而 c、d、e 则可达 10^8 \sim 10^{12}。
若直接使用原始值训练,网络将难以平衡各参数的梯度更新,极易陷入局部最优或震荡。因此,必须对输出标签进行定制化预处理。
为此,我们设计了一套混合尺度归一化策略:
– 对 a 放大 10 倍以提升其在损失函数中的权重;
– 对 b 缩小 10000 倍以避免其主导梯度;
– 对 c、d、e 这类跨越多个数量级的参数,采用带符号的对数变换(\text{sign}(x) \cdot \log_{10}(|x| + \epsilon)),将其压缩到线性可学习范围;
– 最后对所有变换后的参数统一进行 Z-score 标准化(减均值、除标准差),使输入网络的标签近似服从标准正态分布。
这一预处理流程(见 normalize_params)不仅显著提升了训练稳定性,还使得网络能更均衡地学习每个参数的映射关系。更重要的是,我们完整保留了反变换所需的所有统计信息(缩放因子、均值、标准差、是否对数化等),通过 denormalize_params 可无损还原原始物理参数。
其中代码主要为4个函数:
– 根据参数生成幅频相频数据
– 对参数进行预处理作为神经网络训练的输出标签的函数
– 对神经网络输出进行反处理得到实际参数的函数
– 为神经网络加载训练数据的load_data函数
具体代码如下:
import numpy as np
import matplotlib.pyplot as plt
def generate_frequency_response(a, b, c, d, e, f_min=10e3, f_max=100e3, n_freq=32):
"""根据传递函数参数生成频率响应(复数形式)"""
f = np.logspace(np.log10(f_min), np.log10(f_max), n_freq)
w = 2 * np.pi * f
s = 1j * w
numerator = a * s**2 + b * s + c
denominator = s**2 + d * s + e
H = numerator / denominator
return f, H
def normalize_params(Y):
"""
定制化参数归一化:
- a: 放大10倍后直接z-score
- b: 缩小10000倍后直接z-score
- c/d/e: 带符号log10变换后z-score
"""
Y_processed = Y.copy()
# 标记需要log逆变换的参数
is_logged = [False, False, True, True, True] # [a, b, c, d, e]
# 定义缩放系数
a_scale = 10
b_scale = 10000
# 处理a: 放大10倍
Y_processed[:, 0] *= a_scale
# 处理b: 缩小10000倍
Y_processed[:, 1] /= b_scale
# 处理c/d/e: 带符号log10变换
for i in [2, 3, 4]:
sign = np.sign(Y_processed[:, i])
abs_log = np.log10(np.abs(Y_processed[:, i]) + 1e-6) # 避免log(0)
Y_processed[:, i] = sign * abs_log
# 统一z-score归一化
mean = np.mean(Y_processed, axis=0)
std = np.std(Y_processed, axis=0)
Y_norm = (Y_processed - mean) / (std + 1e-8)
# 存储反归一化所需信息
stats = {
"mean": mean,
"std": std,
"is_logged": is_logged,
"a_scale": a_scale,
"b_scale": b_scale
}
return Y_norm, stats
def denormalize_params(Y_norm, stats):
"""反归一化,恢复原始参数尺度"""
# z-score逆变换
Y_processed = Y_norm * stats["std"] + stats["mean"]
Y = Y_processed.copy()
# 对log变换参数执行逆变换
for i in range(5):
if stats["is_logged"][i]:
sign = np.sign(Y_processed[:, i])
abs_exp = 10 ** np.abs(Y_processed[:, i])
Y[:, i] = sign * abs_exp
# 还原a的尺度
Y[:, 0] /= stats["a_scale"]
# 还原b的尺度
Y[:, 1] *= stats["b_scale"]
return Y
def load_data(seed=1984, n_samples=100):
np.random.seed(seed)
f_min, f_max = 10e3, 100e3 # Hz
N_freq = 32
f = np.logspace(np.log10(f_min), np.log10(f_max), N_freq)
w = 2 * np.pi * f
X = []
Y = []
for _ in range(n_samples):
# 生成极点参数
wn = np.random.uniform(2*np.pi*5e3, 2*np.pi*200e3)
zeta = np.random.lognormal(mean=np.log(0.2), sigma=1.0)
zeta = np.clip(zeta, 0.05, 1.5)
K = np.random.lognormal(mean=np.log(1.0), sigma=1.0)
K = np.clip(K, 0.01, 100)
# 生成分子参数
a = np.random.normal(0, 0.1) # 原始尺度≈±0.1
b = np.abs(np.random.normal(0, 1e4)) # 原始尺度≈1e4
c = K * wn**2 # 原始尺度≈1e8~1e12
# 生成分母参数
d = 2 * zeta * wn # 原始尺度≈1e4~1e6
e = wn**2 # 原始尺度≈1e8~1e12
# 计算频率响应
s = 1j * w
H = (a * s**2 + b * s + c) / (s**2 + d * s + e)
x = np.concatenate([H.real, H.imag])
X.append(x)
Y.append([a, b, c, d, e])
X = np.array(X)
Y = np.array(Y)
Y_norm, stats = normalize_params(Y)
# return X, Y_norm, stats, Y
return X, Y_norm, stats
具体网络 HsNet
示意图如图
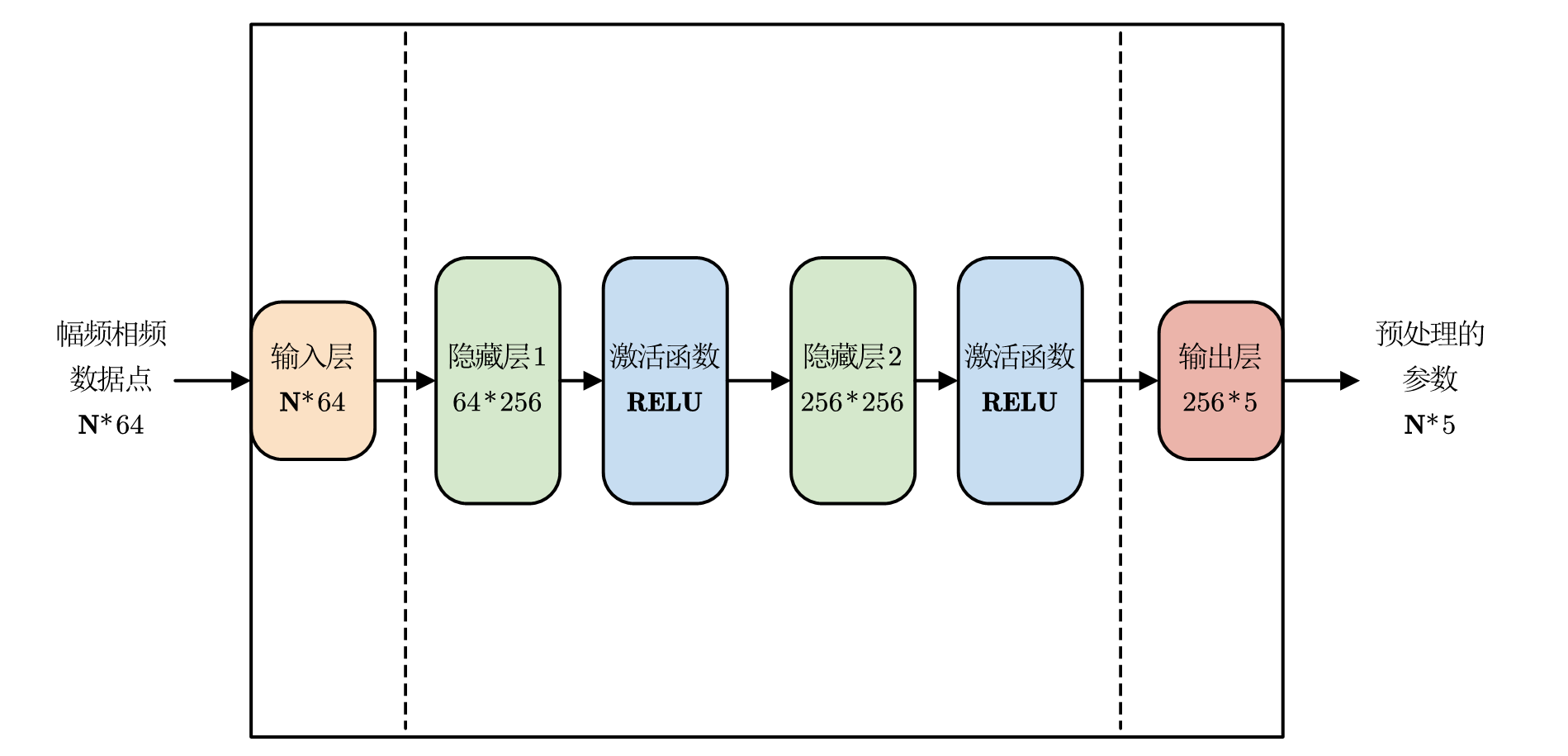
网络主体
import os
import sys
# 将当前工作目录切换到该脚本所在的目录
script_dir = os.path.dirname(os.path.abspath(__file__))
os.chdir(script_dir)
sys.path.append('..')
import numpy as np
from common.layers import Affine, Sigmoid, MSELoss, ReLU
class HsNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
# He 初始化(适合 ReLU)
W1 = np.random.randn(I, H) * np.sqrt(2.0 / I)
b1 = np.zeros(H)
W2 = np.random.randn(H, H) * np.sqrt(2.0 / H) # 第二隐藏层
b2 = np.zeros(H)
W3 = np.random.randn(H, H) * np.sqrt(2.0 / H) # 第二隐藏层
b3 = np.zeros(H)
W4 = np.random.randn(H, O) * np.sqrt(2.0 / H)
b4 = np.zeros(O)
self.layers = [
Affine(W1, b1),
ReLU(),
Affine(W2, b2),
ReLU(),
Affine(W3, b3),
ReLU(),
Affine(W4, b4)
]
self.loss_layer = MSELoss()
self.params = []
self.grads = []
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self, x, t):
x = self.predict(x)
loss = self.loss_layer.forward(x,t)
return loss
def backward(self, dout = 1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
参数读取和保存,作为该对象的类函数。
def save_parameters(self, file_path):
"""
保存模型参数到文件
参数:
file_path: 保存参数的文件路径(通常使用.npz扩展名)
"""
# 创建一个字典来存储所有参数
params_dict = {f'param_{i}': param for i, param in enumerate(self.params)}
# 保存参数
np.savez(file_path, **params_dict)
print(f"参数已保存到 {file_path}")
def load_parameters(self, file_path):
"""
从文件加载模型参数
参数:
file_path: 加载参数的文件路径
"""
if not os.path.exists(file_path):
raise FileNotFoundError(f"参数文件 {file_path} 不存在")
# 加载参数
loaded_data = np.load(file_path)
# 检查加载的参数数量是否与模型预期的一致
if len(loaded_data.files) != len(self.params):
raise ValueError(f"参数数量不匹配: 预期 {len(self.params)} 个, 但文件中有 {len(loaded_data.files)} 个")
# 将加载的参数赋值给模型
for i in range(len(self.params)):
self.params[i] = loaded_data[f'param_{i}']
# 同时更新对应层的参数(因为params是层参数的引用)
# 找到对应的层和参数索引
param_idx = 0
for layer in self.layers:
if hasattr(layer, 'params'):
for j in range(len(layer.params)):
if param_idx == i:
layer.params[j] = self.params[i]
break
param_idx += 1
if param_idx > i:
break
print(f"已从 {file_path} 加载参数")
训练部分及对比演示代码
import os
import sys
script_dir = os.path.dirname(os.path.abspath(__file__))
os.chdir(script_dir)
sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt
# -------------------------- 1. 核心配置:统一存储目录 --------------------------
# 根目录名称(可自定义,如"hsnet_results_2024")
ROOT_SAVE_DIR = "hsnet_training_results"
# 子目录划分(分类存储不同类型文件)
PARAM_SAVE_DIR = os.path.join(ROOT_SAVE_DIR, "model_params") # 模型参数
IMAGE_SAVE_DIR = os.path.join(ROOT_SAVE_DIR, "plots") # 图片
LOSS_SAVE_DIR = os.path.join(ROOT_SAVE_DIR, "loss_data") # 损失数据
# 自动创建所有目录(不存在则创建,避免报错)
for dir_path in [ROOT_SAVE_DIR, PARAM_SAVE_DIR, IMAGE_SAVE_DIR, LOSS_SAVE_DIR]:
if not os.path.exists(dir_path):
os.makedirs(dir_path)
print(f"创建目录: {dir_path}")
# -------------------------- 2. 基础导入与路径配置 --------------------------
# 导入模块
from HsNet import HsNet
from dataset import ch01HsGenerate # 确保返回 (X, Y_norm, stats)
from common.optimizer import Adam, AdamW, ReduceLROnPlateau
# -------------------------- 3. 训练参数设定 --------------------------
max_epoch = 2000
batch_size = 32
hidden_size = 256
learning_rate = 0.001
# 统一文件路径(关联到子目录)
param_save_path = os.path.join(PARAM_SAVE_DIR, "hsnet_trained_params.npz") # 参数文件
loss_save_path = os.path.join(LOSS_SAVE_DIR, "training_loss.npz") # 损失数据文件
# 图片路径(后续绘图时使用)
loss_plot_path = os.path.join(IMAGE_SAVE_DIR, "loss_curve.png")
pred_true_plot_path = os.path.join(IMAGE_SAVE_DIR, "pred_vs_true.png")
freq_response_plot_path = os.path.join(IMAGE_SAVE_DIR, "frequency_response.png")
# -------------------------- 4. 数据加载 --------------------------
data = ch01HsGenerate.load_data(seed = None,n_samples=5000)
if len(data) == 3:
X, Y_norm, stats = data
else:
X, Y_norm = data
stats = None
x_orig = X.copy()
t_orig = Y_norm.copy()
# 数据维度校验
data_size, input_size = X.shape
_, output_size = Y_norm.shape
assert output_size == 5, "输出必须是5维参数!"
iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = [] # 存储所有平均损失(后续保存)
# -------------------------- 5. 模型初始化与预训练加载 --------------------------
model = HsNet(input_size, hidden_size, output_size)
optimizer = AdamW(lr=learning_rate, weight_decay = 0.01)
scheduler = ReduceLROnPlateau(optimizer, mode='min', factor=0.5, patience=100, verbose=True)
# 加载预训练模型(可选)
load_pretrained = False
if os.path.exists(param_save_path):
choice = input(f"发现预训练参数文件 {param_save_path}\n是否加载并跳过训练?(y/n): ").lower()
if choice == "y":
model.load_parameters(param_save_path)
load_pretrained = True
# 若存在保存的损失数据,加载到loss_list(用于绘图)
if os.path.exists(loss_save_path):
loss_list = np.load(loss_save_path)["loss_list"].tolist()
print(f"已加载历史损失数据(共{len(loss_list)}个记录点)")
# -------------------------- 6. 训练循环(仅当未加载预训练时执行) --------------------------
if not load_pretrained:
print("\n开始训练...")
if not load_pretrained:
print("\n开始训练(每次epoch动态生成新数据)...")
total_loss = 0
loss_count = 0
for epoch in range(max_epoch):
# ✅ 关键修改:每次epoch动态生成新训练数据
train_data = ch01HsGenerate.load_data(seed=None, n_samples=5000) # seed=None 确保随机性
if len(train_data) == 3:
X, Y_norm, _ = train_data # 忽略stats,训练用归一化数据即可
else:
X, Y_norm = train_data
data_size = X.shape[0]
iters = data_size // batch_size
# 随机打乱(虽然load_data已随机,但再打乱更稳妥)
idx = np.random.permutation(data_size)
X_shuffled = X[idx]
Y_shuffled = Y_norm[idx]
epoch_loss = 0
for iter in range(iters):
batch_x = X_shuffled[iter * batch_size : (iter + 1) * batch_size]
batch_t = Y_shuffled[iter * batch_size : (iter + 1) * batch_size]
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
epoch_loss += loss
total_loss += loss
loss_count += 1
if loss_count % 10 == 0:
avg_loss = total_loss / loss_count
loss_list.append(avg_loss)
total_loss = 0
loss_count = 0
print(f'| epoch {epoch + 1:4d} | iter {iter + 1:3d}/{iters} | loss {avg_loss:.6f}')
# 每个epoch结束后更新学习率(基于epoch平均损失)
avg_epoch_loss = epoch_loss / iters
scheduler.step(avg_epoch_loss)
# -------------------------- 6.1 训练后保存:参数 + 损失 --------------------------
# 保存模型参数
model.save_parameters(param_save_path)
# 保存损失数据(用npz格式,方便后续加载)
np.savez(loss_save_path, loss_list=np.array(loss_list))
print(f"\n损失数据已保存到: {loss_save_path}")
plt.figure(figsize=(10, 4))
plt.plot(loss_list, label='Training Loss (Avg per 10 Iters)', color='purple', linewidth=1.5)
plt.xlabel('Iteration Groups (×10 Iters)', fontsize=10)
plt.ylabel('MSE Loss', fontsize=10)
plt.title('HsNet Training Loss Curve', fontsize=12, fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(fontsize=9)
plt.tight_layout() # 自动调整布局,避免标签被截断
plt.savefig(loss_plot_path, dpi=300, bbox_inches='tight') # dpi=300确保高清
plt.close() # 关闭画布,避免内存占用
print(f"损失曲线已保存到: {loss_plot_path}")
# -------------------------- 7. 结果可视化:绘图并保存到图片目录 --------------------------
print("\n开始生成可视化结果...")
# -------------------------- 7.1 1. 损失曲线(保存到IMAGE_SAVE_DIR) --------------------------
# -------------------------- 7.2 2. 预测值 vs 真实值(5个子图,保存到IMAGE_SAVE_DIR) --------------------------
# 模型预测(用原始数据)
Y_pred_norm = model.predict(x_orig)
# 反归一化到物理参数(若有stats)
if stats is not None:
Y_pred = ch01HsGenerate.denormalize_params(Y_pred_norm, stats)
Y_true = ch01HsGenerate.denormalize_params(t_orig, stats)
else:
Y_pred = Y_pred_norm
Y_true = t_orig
# 参数名称(与你的5维输出对应)
param_names = ['b₀ (num s²)', 'b₁ (num s)', 'b₂ (num const)', 'a₁ (den s)', 'a₂ (den const)']
plt.figure(figsize=(15, 10))
for i in range(5):
plt.subplot(2, 3, i + 1) # 2行3列布局,空出第6个子图
# 提取当前参数的真实值和预测值
true_vals = Y_true[:, i]
pred_vals = Y_pred[:, i]
# 绘制散点图
plt.scatter(true_vals, pred_vals, alpha=0.6, s=20, color='orange', label='Predicted', zorder=2)
plt.scatter(true_vals, true_vals, alpha=0.4, s=10, color='blue', marker='x', label='True (Ref)', zorder=1)
# 绘制理想参考线(y=x)
min_val = min(true_vals.min(), pred_vals.min()) * 0.95 # 留少量边距
max_val = max(true_vals.max(), pred_vals.max()) * 1.05
plt.plot([min_val, max_val], [min_val, max_val], 'k--', linewidth=1.2, label='Ideal: Pred=True', zorder=3)
# 标签与格式
plt.xlabel('True Value', fontsize=9)
plt.ylabel('Predicted Value', fontsize=9)
plt.title(f'Parameter: {param_names[i]}', fontsize=10, fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.5)
plt.legend(fontsize=8)
# 删除第6个空的子图(2行3列,最后一个位置)
plt.delaxes(plt.subplot(2, 3, 6))
plt.tight_layout()
plt.savefig(pred_true_plot_path, dpi=300, bbox_inches='tight')
plt.close()
print(f"预测vs真实值图已保存到: {pred_true_plot_path}")
# -------------------------- 7.3 3. 幅频/相频响应对比(保存到IMAGE_SAVE_DIR) --------------------------
# 频率设置(与数据生成逻辑一致)
f_min, f_max = 10e3, 100e3 # Hz
N_freq = 32
f = np.logspace(np.log10(f_min), np.log10(f_max), N_freq) # 对数均分频率
w = 2 * np.pi * f # 角频率
# 随机选3个样本进行对比(固定seed确保结果可复现)
# np.random.seed(42)
sample_indices = np.random.choice(len(x_orig), size=3, replace=False)
plt.figure(figsize=(16, 12))
for idx, sample_i in enumerate(sample_indices):
# 获取当前样本的真实参数和预测参数
y_true = Y_true[sample_i] # [b0, b1, b2, a1, a2]
y_pred = Y_pred[sample_i]
b0_t, b1_t, b2_t, a1_t, a2_t = y_true
b0_p, b1_p, b2_p, a1_p, a2_p = y_pred
# 计算频率响应(复数值)
s = 1j * w
H_true = (b0_t * s**2 + b1_t * s + b2_t) / (s**2 + a1_t * s + a2_t)
H_pred = (b0_p * s**2 + b1_p * s + b2_p) / (s**2 + a1_p * s + a2_p)
# 转换为幅值(dB)和相位(度)
mag_true = 20 * np.log10(np.abs(H_true) + 1e-12) # +1e-12避免log(0)
phase_true = np.angle(H_true, deg=True)
mag_pred = 20 * np.log10(np.abs(H_pred) + 1e-12)
phase_pred = np.angle(H_pred, deg=True)
# 幅频响应子图(左列)
plt.subplot(3, 2, 2*idx + 1)
plt.semilogx(f/1e3, mag_true, 'b-', linewidth=2.5, label='True System', zorder=2)
plt.semilogx(f/1e3, mag_pred, 'r--', linewidth=2, label='Predicted System', zorder=3)
plt.title(f'Sample {sample_i}: Magnitude Response', fontsize=11, fontweight='bold')
plt.xlabel('Frequency (kHz)', fontsize=9)
plt.ylabel('Magnitude (dB)', fontsize=9)
plt.grid(True, which="both", ls="--", alpha=0.7) # 对数坐标网格
plt.legend(fontsize=9)
# 相频响应子图(右列)
plt.subplot(3, 2, 2*idx + 2)
plt.semilogx(f/1e3, phase_true, 'b-', linewidth=2.5, label='True System', zorder=2)
plt.semilogx(f/1e3, phase_pred, 'r--', linewidth=2, label='Predicted System', zorder=3)
plt.title(f'Sample {sample_i}: Phase Response', fontsize=11, fontweight='bold')
plt.xlabel('Frequency (kHz)', fontsize=9)
plt.ylabel('Phase (degrees)', fontsize=9)
plt.grid(True, which="both", ls="--", alpha=0.7)
plt.legend(fontsize=9)
plt.tight_layout()
plt.savefig(freq_response_plot_path, dpi=300, bbox_inches='tight')
plt.close()
print(f"频率响应图已保存到: {freq_response_plot_path}")
# -------------------------- 8. 最终结果输出 --------------------------
# 计算最终损失(用全部原始数据)
final_loss = model.forward(x_orig, t_orig)
print(f"\n==================== 训练/评估完成 ====================")
print(f"最终归一化MSE损失: {final_loss:.6f}")
print(f"\n所有文件保存目录: {os.path.abspath(ROOT_SAVE_DIR)}")
print(f"1. 模型参数: {os.path.basename(param_save_path)}")
print(f"2. 损失数据: {os.path.basename(loss_save_path)}")
print(f"3. 可视化图片: {os.listdir(IMAGE_SAVE_DIR)}")
—
初版结果演示
按照上述代码配置,使用cpu训练一轮约半小时。
训练损失展示
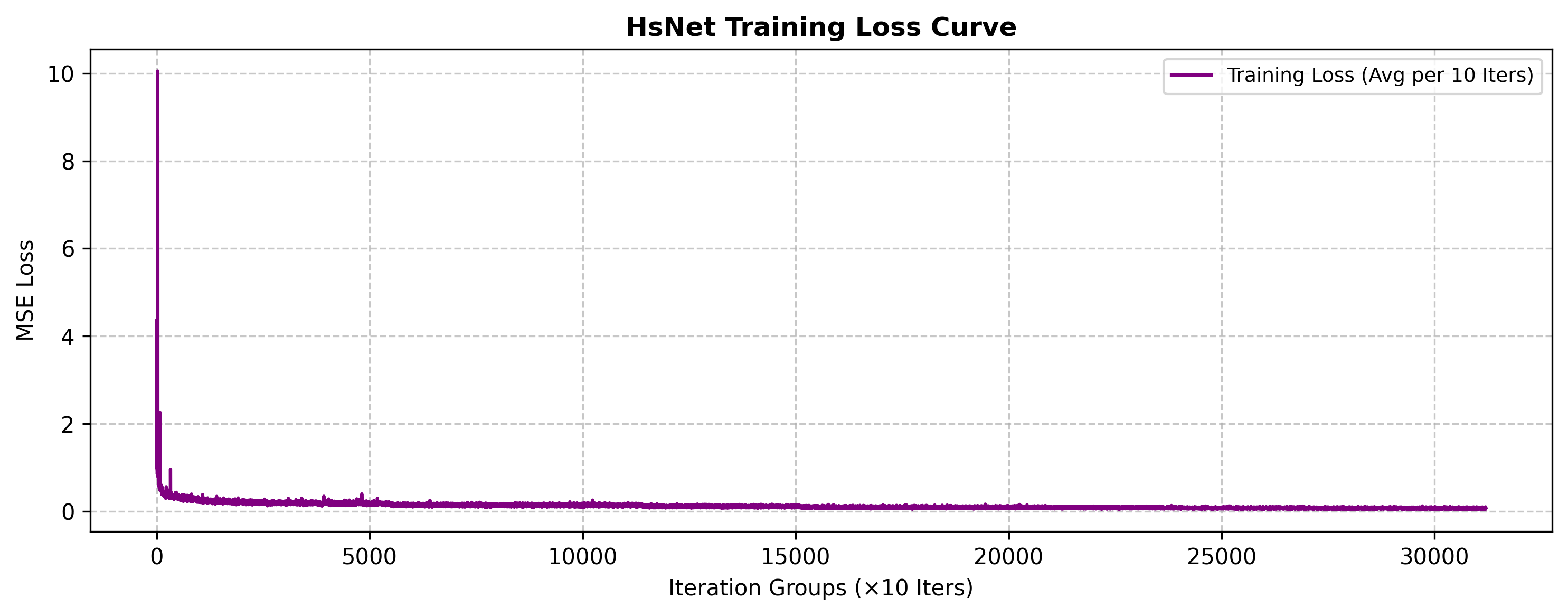
可以发现当前网络其实很早就收敛了,没法进一步继续收敛,或许增加网络深度或训练轮次仍可以进一步改进。
参数逆处理后比较

可以发现除了参数b,acde参数都得到了良好的拟合和预测,预计实际拟合的误差主要还是参数b导致的,仍可以改进
随机真实值与预测值比较
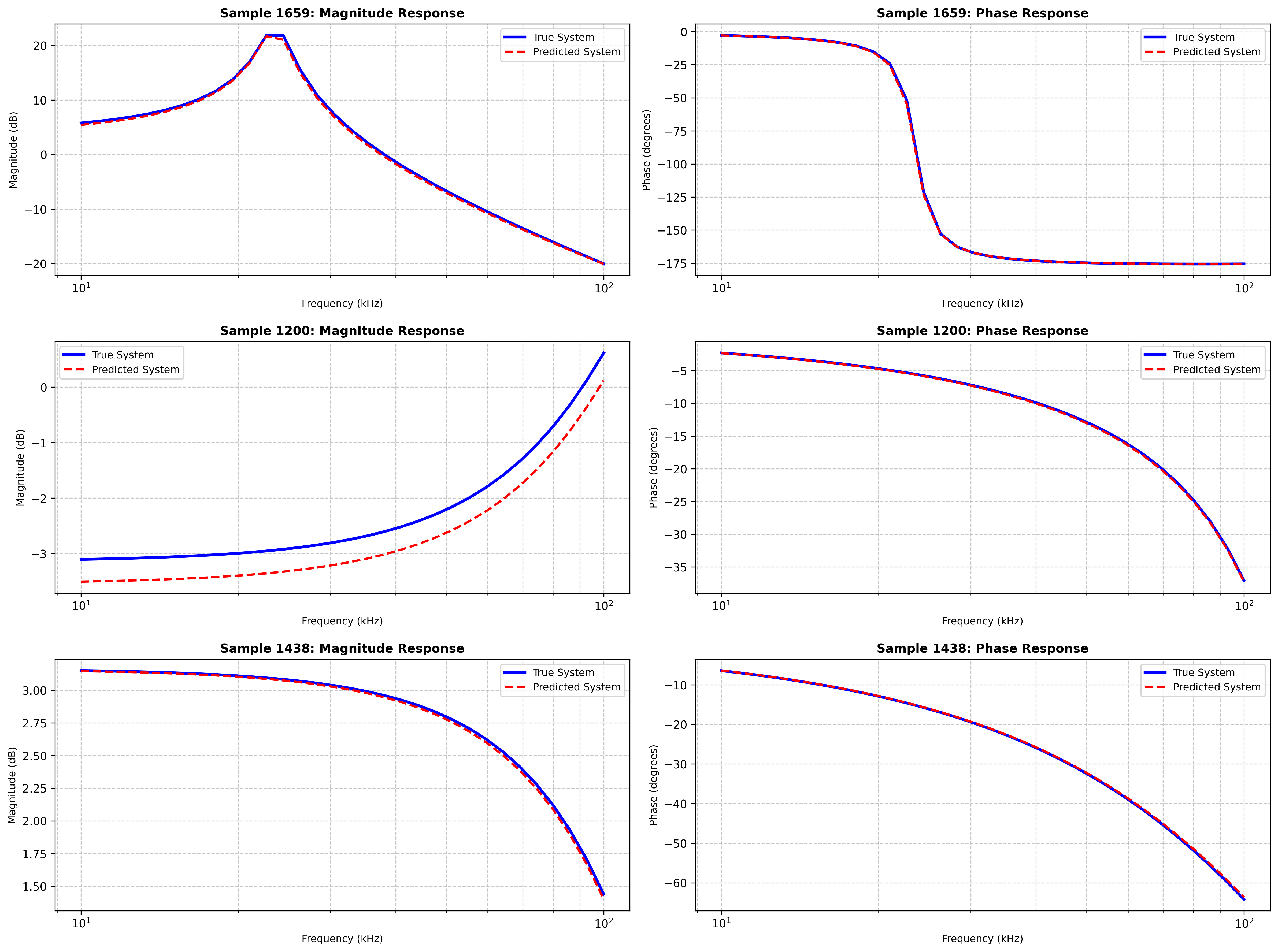

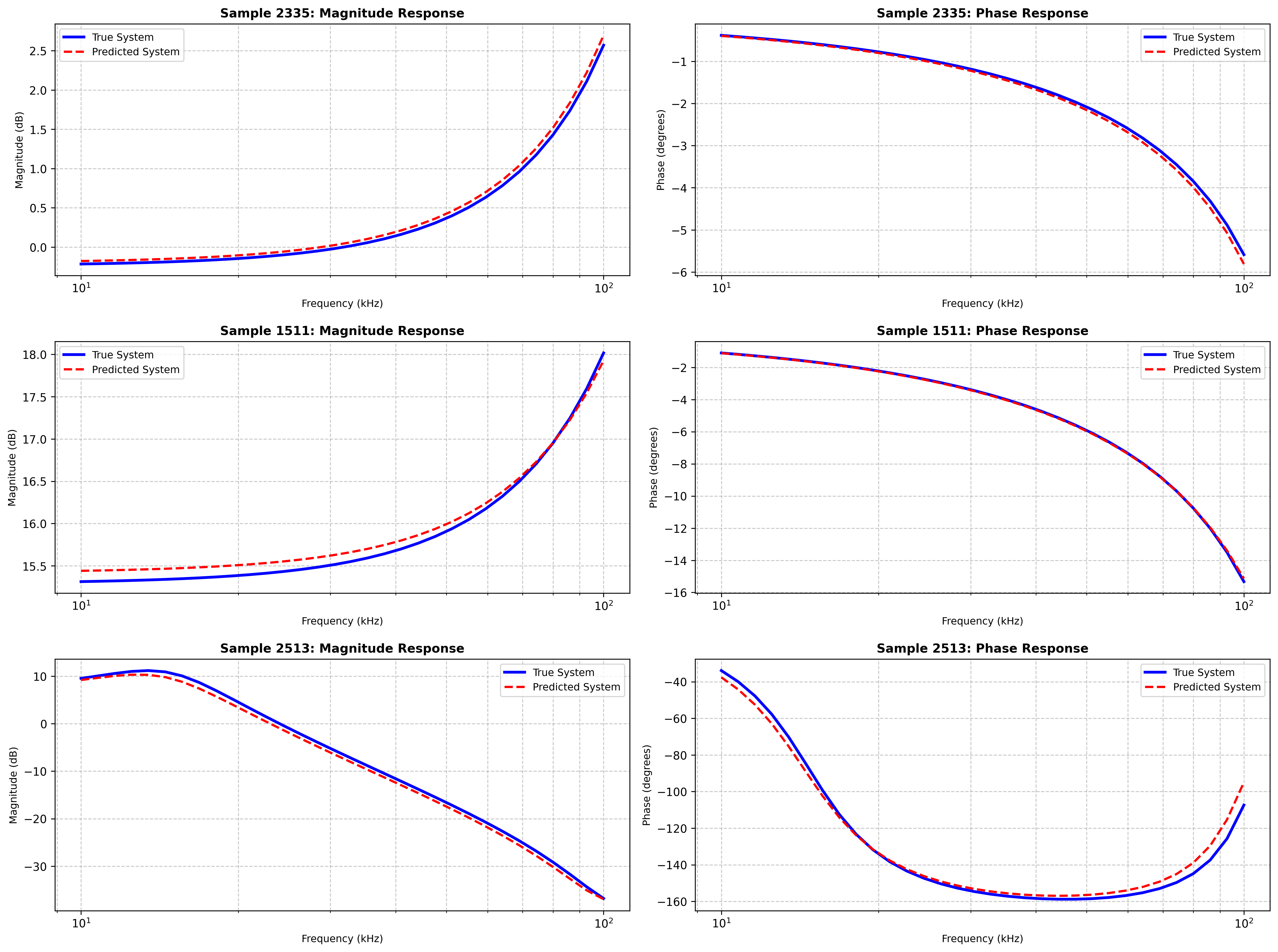

可以发现幅频相频曲线基本拟合,但仍存在微小偏差可以改进优化。
python代码链接
通过网盘分享的文件:20251013HsProject.zip
链接: https://pan.baidu.com/s/163YAoPkYVgLyKyyk-zhz5g 提取码: 355k
主要参考书目:
《深度学习入门:基于Python的理论与实现》
《深度学习进阶:自然语言处理》
****其中代码风格也是仿照它的***